Cùng cùng với 7 hằng đẳng thức đáng nhớ, những hằng đẳng thức mở rộng cũng khá được áp dụng các vào giải quyết và xử lý các bài toán trong đại số cũng như hình học. Hãy cùng ongirlgames.com khám phá những hằng đẳng thức mở rộng, cũng giống như cách chứng tỏ nhé!
Các hằng đẳng thức mở rộng cơ bản
Hằng đẳng thức bậc 2 mở rộng lớn
((a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc)((a+b-c)^2=a^2+b^2+c^2+2ab-2ac-2bc)((a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd)Hằng đẳng thức bậc 3 mở rộng
((a+b+c)^3=a^3+b^3+c^3+3(a+b)(a+c)(b+c))(a^3+b^3=(a+b)^3-3ab(a+b))(a^3-b^3=(a-b)^3+3ab(a-b))(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-ac-bc))Hằng đẳng thức bậc 4 mở rộng
((a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4)Hằng đẳng thức bậc 5 mở rộng
((a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5)Hằng đẳng thức bậc 6 mở rộng
((a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6)Hằng đẳng thức bậc 7 mở rộng
((a+b)^7=a^7+7a^6b+21a^5b^2+35a^4b^3+35a^3b^4+21a^2b^5+7ab^6+b^7)
Các hằng đẳng thức mở rộng nâng cao
Bình phương của (n) số hạng ((n>2))
((a_1+a_2+a_3+…+a_n-1+a_n)^2=a_1^2+a_2^2+a_3^2+…+a_n^2+2a_1a_2+2a_1a_3+…+2a_1a_n+2a_2a_3…+a_n-1a_n)Hằng đẳng thức (a^n+b^n) ( cùng với n là số lẻ)(a^n+b^n=(a+b)(a^n-1-a^n-2b+a^n-3b^2+…+b^n-1))Hằng đẳng thức (a^n-b^n) ( với n là số lẻ)
(a^n-b^n=(a-b)(a^n-1+a^n-2b+a^n-3b^2+…+b^n-1))Hằng đẳng thức (a^n-b^n) (với n là số chẵn)
(a^n-b^n=(a-b)(a^n-1+a^n-2b+a^n-3b^2+…+b^n-1))hoặc: (=(a+b)(a^n-1-a^n-2b+a^n-3b^2+…-b^n-1))
Cách nhớ:
***Lưu ý: gặp mặt bài toán tất cả công thức (a^n-b^n) (với n là số chẵn) hãy nhớ cho công thức:
(a^2-b^2=(a+b)(a-b)) (viết ((a+b)) trước )(a^2-b^2=(a-b)(a+b)) ( viết ((a-b)) trước ).Bạn đang xem: Các hằng đẳng thức nâng cao
Chú ý: chạm chán bài toán (a^n+b^n) ( cùng với n là số chẵn) hãy nhớ
(a^2+b^2) không tồn tại công thức tổng quát đổi khác thành tích. Tuy thế một vài trường hợp đặc trưng có số mũ bởi 4k tất cả thể chuyển đổi thành tích được.
Xem thêm: 5 Phim Hồ Ly Chín Đuôi Là Gì, Tại Sao Người Hàn Quốc Lại Sợ Hãi?
Nhị thức Newton với tam giác Pascal
Khai triển ((A+B)) để viết bên dưới dạng một nhiều thức cùng với lũy thừa bớt dần của A theo lần lượt với (n= 0;1;2;3,…)
Ta được:
((A+B)^0=1)((A+B)^1=A+1B)((A+B)^2=A^2+2AB+B^2)((A+B)^3=A^3+3A^2B++3AB^2+B^3)((A+B)^4=A^4+4A^3B+6A^2B^2+4AB^3+B^4)((A+B)^5=A^5+5A^4B+10A^3B^2+10A^2B^3+5AB^4+B^5)| (n=0) | (1) |
| (n=1) | 1 1 |
| (n=2) | 1 2 1 |
| (n=3) | 1 3 3 1 |
| (n=4) | 1 4 6 4 1 |
| (n=5) | 1 5 10 10 5 1
|
| … | … |
Nhờ đó, suy ra:
((A+B)^6=A^6+6A^5B+15A^4B^2+20A^3B^3+15A^2B^4+6AB^5+B^6)
Bảng các hệ số trên gọi là Tam giác Pascal (nhà toán học tập Pascal (1623-1662)).
Nhà chưng học lỗi lạc Newton (1643-1727) đã giới thiệu công thức tổng quát sau:
((A+B)^n=A^n+nA^n-1B+fracn(n-1)1.2A^n-2B^2+fracn(n-1)(n-2)1.2.3A^n-3B^3+…+fracn(n-1)1.2A^2B^n-2+nAB^n-1+B^n)
Chứng minh hằng đẳng thức mở rộng
Dưới đây là cách chứng tỏ hằng đẳng thức mở rộng đơn giản và nhanh nhất.
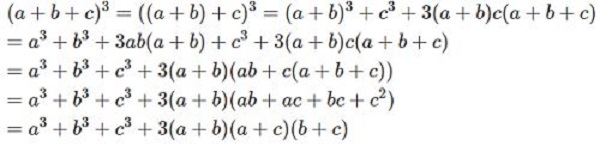
Trên đây là kiến thức tổng hòa hợp về hằng đẳng thức cơ bản và nâng cấp với kỹ năng và kiến thức mở rộng, hy vọng cung ứng cho các bạn những kiến thức và kỹ năng hữu ích trong quá trình học tập của bản thân. Giả dụ thấy nội dung bài viết chủ đề hằng đẳng thức không ngừng mở rộng này thú vị, hãy nhờ rằng share lại nha những bạn! Chúc chúng ta luôn học tập tốt!



